继续上一节讲“天圆地方”原理的应用。
圆出于方,方出于矩, 矩出于九九八十一。
故折矩,以为句,广三, 股修四, 径隅五。
既方其外,半之一矩。 环而共盘,得成三四五。
两矩共长二十有五,是谓积矩。
故禹之所以治天下者,此数之所生也。
这里出现了有名的“勾股定理”,西方叫做毕达哥拉斯定理。商高是西周人,约在公元前的1000年左右,而西方最早可以追溯到古希腊的毕达哥拉斯学派,约公元前6世纪至公元前5世纪。该学派的创始人是毕达哥拉斯,他们的证明可能是基于几何图形和直观推理,没有使用严格的数学符号,当然在《周髀算经》中商高也未给出等式证明。
现代数学讲究的是在已有的数学体系下,去论证其它的公式定理,以便于使这些公式能够最终到应用层面,本身也没错。
并不是以前的人不能给出你现代的证明方式,就是不懂这些道理。
可以通过“矩”的折痕,来得出“广三, 股修四, 径隅五”:
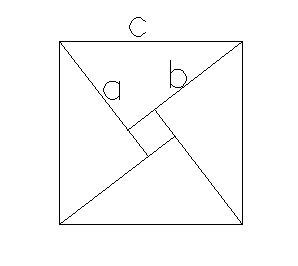
只要能折出直角三角形,就可以确定它们的面积,通过面积计算得出c的2次方=(b-a)的2次方+2ab=a的2次方+b的2次方。
确定了直角三角形的三边关系之后,当采用立杆测影时,选取一个参考点,《周髀算经》是周地,也是周代时某个测天文的根据地。立杆是垂直于地面的,而古人思维中的“天”也是垂直于地面的,这样形成了两个相似三角形。立杆由于不同的光照角度,会形成日影,日影的长度可测定,立杆一般为8尺,那小三角的第三边可以算出来。周地到立杆的距离可以事先确定,比如3公里,5公里,这样“天”到立杆地的距离便可以算出来。当然这里的“天”并不等于太阳。
所以,古人第一步便要确定这个模型内,“尺寸”与距离“里”的换算比例。于是有下面这个实验步骤:
周髀长八尺,夏至之日晷一尺六寸。髀者,股也。正晷者,句也。正南千里,句一尺五寸。正北千里,句一尺七寸。日益表南,晷日益长。
选取和制作一个长度为8尺的测竿,在正中午时,立杆测影,此时日影与假定的地平面垂直。在夏至日正午观测到日影长1尺6寸,将测竿往离周地正南距离1000里的地方移动,测得日影长1尺5寸。将测竿往相反方向移动1000里,测得日影长1尺7寸。
那这种操作方式之下,就得出了一个比例关系,也就是1000里=1寸,寸影千里。这种等式的实验结果,需要在地球特定的纬度之上,得在北纬36°左右,才能得出1尺6寸,历代都对这个日影长度的数据进行过考证。
得出了日影长度与距离的比例关系,那么古典天文学背景下的“天、地”距离就很好测定了。
“禹之所以治天下者,此数之所生”,说明这种测定方式,或者勾股定理,早在大禹时代就开始运用了,大禹还属于三皇五帝时期人物,其治水方法:根据山脉地形,采用疏导治水的方法,开沟掘渠,使洪水从江河流入大海。
也就是他老爸鲧采用堵洪水的方式,而大禹采用疏通引导的方式。无论是“堵”还是“引流”,都要在需要保护的地方建造大坝,来挡住洪水的冲击,而建造堤坝,必须得有基本的建筑构造数学知识,相信在很早之前古人就已经在运用这些计算方式。