僅僅通過“意念”,而不依靠其它媒介影響世界,這種超自然現象會被人想當然的視為偽科學。然而這在國外的超心理現象研究中是一個重要的領域,其中用意念影響亂數發生器(RNG),是最為成熟的一種研究“意念力”的方法。
昨天看到一篇2006年的心理學綜述文章,對近幾十年超心理研究中,意念影響亂數發生器的研究報告進行薈萃分析(文章的PDF在此),發表的雜誌是Psychological Bulletin,影響因數13,在全世界的心理學雜誌中排名前五。薈萃分析的結論是:意念會對RNG產生微弱的影響,這種影響具有非常顯著的統計學意義。在如此高級別的期刊上發表肯定超心理研究結論的文章,一定會讓那些科學主義者,比如方舟子之流驚掉下巴。
用意念影響亂數發生器的想法是物理學家搞出來的,上世紀70年代,麻省理工大學一些腦洞大開的物理學家認為,既然在哥本哈根學派對量子力學的解釋中,微觀世界離子的行為與人的觀測(意識)有關,疊加態的塌縮與否取決於人的觀測,那麼意識有沒有可能不通過觀測而直接作用於微觀粒子呢?於是就設計了一種基於量子效應的亂數發生器,並進行了大量意念影響RNG的實驗,1986年他們報導了為期7年,對33個受試的數百萬次測試的結果。(Jahn R G & B J Dunne
,On the Quantum Mechanics of Consciousness,with Application to Anomalous Phenomena,Foundations of Physics,16,721-772)
顯然,這個研究並未引起物理同行的注意(我也覺得用這種方法去驗證哥本哈根學派的解釋太不可靠了),但卻對超心理研究產生了很大影響。
在使用RNG之前,超心理研究有一種測試意念力(PK)的方法,就是意念影響骰子的點數,這種實驗研究一直可以追溯到19世紀,一百多年中一直有心理學家進行這方面的實驗,積累了不少數據,也有高品質的薈萃分析,結論是意念可以對骰子產生微弱影響,但統計意義顯著。但用骰子實驗操作非常麻煩,要有人擲骰子,要有人記錄,中間的干擾因素也很多。自從物理學家發現了意念可以影響RNG後,RNG就徹底替代了骰子。亂數的生成管道也不再基於量子效應,可以是基於熱譟音,電子譟音等等。可以說這項研究完全脫離了量子力學研究的初衷,成為超心理學的重要方法——儘管超心理學研究者經常引用量子力學的觀念來解釋“超自然”現象。
這就是“意念力”(PK)影響亂數發生器(RNG)實驗的歷史背景。
既然如此多的人進行過這項實驗,都能得到肯定性的實驗結果,而且其薈萃分析能發表在影響因數13的期刊上,我覺得這個問題就不能等閒視之了,我决定自己動手來做這個實驗。
首先,去哪裡找亂數發生器?上網查到intel的cpu就內寘有真亂數發生器,所以要做這個實驗非常簡單,只要用pip安裝一個rdrand包就可以把RNG搞定。
其次,如何設計實驗?
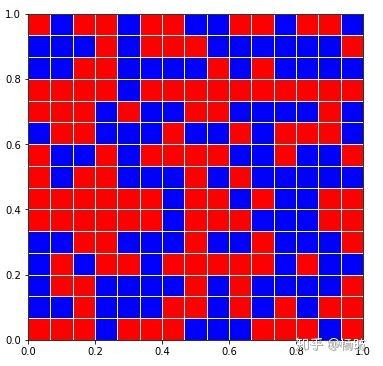
我的方法是生成一組1和0構成的亂數,然後用紅色方塊表示1,用藍色方塊表示0,若干方塊構成一個15×15的大正方形(如圖)。
實驗開始時,我先在腦中閉目想像把藍色方塊逐漸變為紅色方塊,同時默念“紅色,紅色”,然後按下回車,於是電腦開始生成亂數,再按亂數生成圖片,並顯示出紅色方塊的數量作為迴響。然後再閉目想像,按回車……,如此10張圖片為一組。
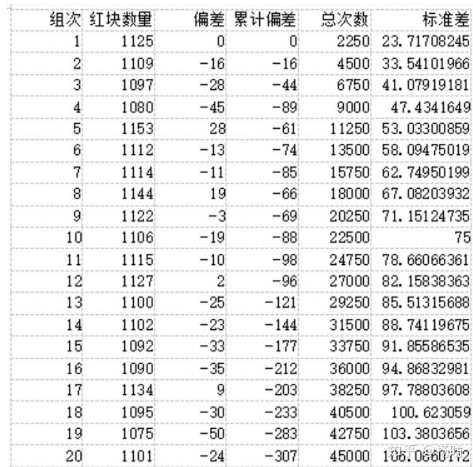
我一共進行了20組實驗,結果如下:
第一列是實驗的組次,每組應該生成15x15x10=2250個方塊,第二列是其中紅色方塊的數量,理論上這個數量的平均值應該是1125,第三列是紅色方塊數偏離1125的數量,第四列是累計偏離數量,第五列是生成紅藍方塊的總數量,第列是偏離數量的標準差。
實驗結果是:經過意念干擾後,紅色方塊出現的概率為0.4932,對應理論的二項式分佈的標準差為0.00236,偏離理論平均值的程度為2.89倍標準差,實驗結果與理論平均值無差异的概率小於p< 0.05,作為一個非常粗糙的預實驗,能取得這樣的結果已經很滿意了。
需要說明的是:
1.雖然我腦子裏想像的是盡可能讓藍色方塊變為紅色方塊,心中也默念的是“紅色,紅色”,但實驗結果是藍色方塊的數量多於紅色。結果和我的意念相反,但p< 0.05的估算已經考慮了雙側效應,不能排除意念對RNG有實質影響的可能,只是意念影響的管道和原來預期的不一樣。
2. 20組實驗是分兩次完成的,前十組在上午,由於昨天讀超心理的文獻到深夜,然後失眠,所以今天早上的精神狀態並不太好。下午充分午休之後,進行的後面十次實驗。
上下午的實驗結果有明顯差异,如果單獨算兩組的平均值和標準差,那麼上午只偏離了1.17倍標準差,而下午偏離了2.92倍標準差。前者沒有統計意義,後者則出現了顯著的統計意義。
下午實驗,除了精神狀態更好之外,還有一個原因是經過上午練習,熟悉了整個流程,而且似乎摸索到了一些意念控制的技巧:
首先是紅色方塊逐漸替代藍色的想像,在腦中更加穩定清晰了。
其次,在按下回車那一瞬間要盡可能集中意念。
再次,下午開始,接受了紅色方塊較少的事實,然後每次實驗要看一眼電腦顯示的紅色方塊數量,想像要得到一個更低的數。
再次,兩次實驗之間要稍微放鬆一下。
一點體會:熟練了這些技巧後,實驗到後面幾輪時,幾乎每按一次回車鍵,都會得到一個小於平均值的紅色方塊數,感覺人的後脊背都在嗖嗖冒涼氣,畢竟前面只是通過文獻知道有這麼一種效應,而且也不太確定自己的實驗方案是否有問題,只是抱著試試看的態度。現在切身感受到自己似乎真的掌握了一些用意念控制環境的方法,就感到後背發凉。
可能有朋友會問,為什麼不做更多輪次實驗,得到更加確定的結果?
因為我只是想驗證一下,Psychological Bulletin那篇文章的結論自己是否可以複現,並不想通過這個實驗證明什麼事情,得到現時這個結果我已經比較滿意了。
其次,做這個實驗比較費精力,要全神貫注,而且也很枯燥,也有點費時間。同時心底也略有恐懼,要真的通過反復練習,掌握了控制意念力的技巧,會不會對身體有傷害?(比如所謂“耗傷元氣”?)
再次,我覺得這個實驗還有不少需要改進優化的地方,比如加入獎懲迴響,優化實驗流程等等,畢竟從我動手設計實驗,到正式開始實驗用了還不到一個小時的時間(主要就是寫程式碼)。
最後,貼出我實驗用的python程式碼,如果你有興趣的話也不妨試試(注意,電腦必須是intel的cpu):
import rdrand as rd
import matplotlib.pyplot as plt
from IPython import display
%matplotlib inline
def get_rnd(rows=10):
ret = []
for i in range(rows*rows):
ret.append(rd.rdrand_get_bits(1))
return ret
def show_img(rnd,rows=10):
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111)
scl = 1 / rows
idx = 0
color_true = 'red'
color_false = 'blue'
count = 0
for x in range(rows):
for y in range(rows):
color = color_true if rnd[idx] == 1 else color_false
count += rnd[idx]
px = scl * x
py = scl * y
rect = plt.Rectangle((scl * x,scl * y),scl,scl,edgecolor='white',facecolor=color)
ax.add_patch(rect)
idx += 1
plt.show()
return count
def exam(row,times):
input(“請想像生成一個紅色圖案,按回車:”)
ret = []
count = 0
num = 0
for i in range(times):
input(“回車開始:”)
display.clear_output(wait=True)
rnd = get_rnd(row)
cnt = show_img(rnd,row)
ret.append((cnt,len(rnd)))
count += cnt
num += len(rnd)
print(cnt,len(rnd))
return count,num,ret
def test_rnd(row,times):
num = 0
count = 0
for i in range(times):
rnd = get_rnd(row)
cnt = show_img(rnd,row)
count += cnt
num += len(rnd)
display.clear_output(wait=True)
return num,count
#測試亂數分佈
#print(test_rnd(15,200))
#開始一組實驗
exam(15,10)